Using "Self" and Special Methods (Constructor)
The "Self" Keyword
The "self" keyword is one major difference between a method (defined inside a class) and function (defined outside a class)."Self" keyword refers to the instance of the object been created. In other words, "self" is replaced by the name of the object when the object is created/instantiated.
The "self" is like "this" keyword in other programming languages such as C++ and PHP.
Any name can be used in place of "self", but python convention requires we use the word "self". It make your code easier to read by other python developers.
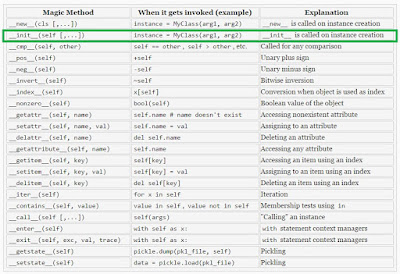
Magic Methods
Magic Methods are special methods in python (that Python invokes when you use certain syntax) with double underscores at the beginning and the end.They're everything in object-oriented Python. They're special methods that you can define to add "magic" to your classes. They're always surrounded by double underscores (e.g. __init__ or __del__).
There many types of magic methods as you can see some listed in image above. The one we are going to use now is the "__init__".
__init__, it is pronouced as: "Underscore underscore init underscore underscore" or "Double underscore init double underscore".
Read more about Magic Methods here:-
~ A Guide to Python's Magic Methods
~ Magic Methods and Operator Overloading
~ Special Method Names
Now back to our Cars object example; lets improve our code from Part 3 to be in a more OOP style by using "self" and "__init__" special magic method.
The only parts of the code that will change from that of the previous section are the: class attributes and object creation parts as seen below.
class Cars:
# Create and Set the class attributes using constructor (__init__) method
def __init__(self, brand, speed, height, weight, colour):
self.brand = brand
self.speed = speed
self.height = height
self.weight = weight
self.colour = colour
# Create the methods with simple "print" statement in them
def activateHorn(self):
print ( self.brand + " Says: Poooooooorh!")
def moveForward(self):
print ( self.brand + " Moving Forward at the speed of: " + self.speed)
def moveBack(self):
print ( self.colour + " " + self.brand + " is Moving Backward!")
def turnRight(self):
print ("Turning Right!")
def turnLeft(self):
print ("Turning Left!")
# Creates First object car1 and Assign the attributes value of car1 object
car1 = Cars("Toyota", "250km/hr", "1908mm", "2800kg", "Green")
# Creates Second object car2 and Assign the attributes value of car2 object
car2 = Cars("Honda", "180km/hr", "1500mm", "3200kg", "Cyan")
# Creates Third object car3 and Assign the attributes value of car3 object
car3 = Cars("Ford", "300km/hr", "2200mm", "4200kg", "Red")
# Call any of the methods on any of the objects to see result
car1.activateHorn()
car2.activateHorn()
car3.activateHorn()
Our code is now more elegant, shorter, and cleaner.
In the next Part 5, we will make our code above even better. By separating the class creation code and class usage (object) code in separate files.
An "import" statement will then be used to communicate between the two files. See you in Part 5.
Reference Materials are here
No comments:
Post a Comment